By how much is my smart watch overestimating my distance?

If you happens to run and own a smart watch with GPS tracking, you might have noticed that depending on the quality of the GPS, the track registered by the smart watch does not exactly match the real track you followed.

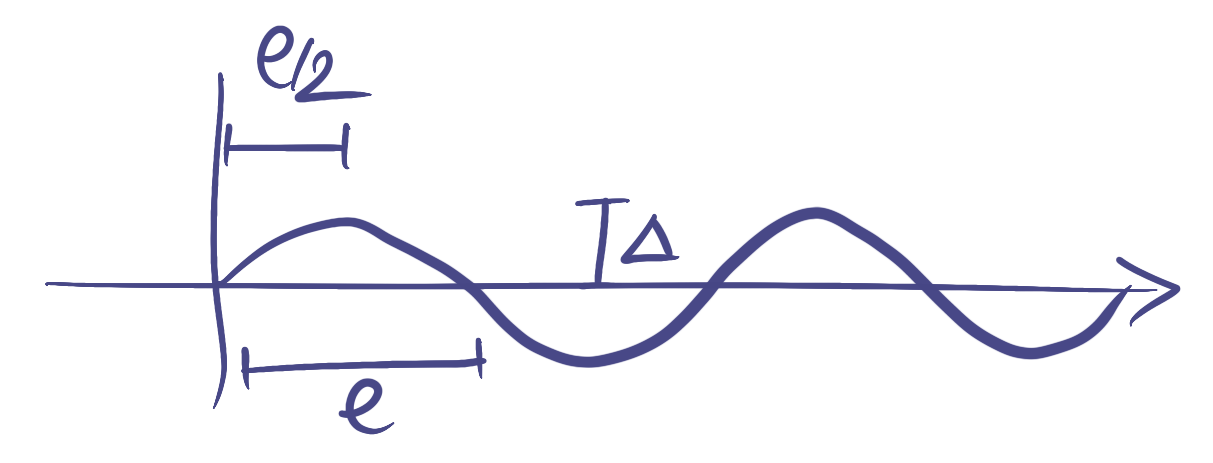
In my case, I noticed that my (poor quality) watch does tend to oscillate around the trajectory I really followed. In particular, when I run alongside a road, it tends to report that I switched side repeatedly, as if I followed a sinusoidal track, like so:

After noticing that, I started to doubt the distance reported by my watch. By how much my watch has been overestimating my performance all these years?

Stating the problem

Looking at the GPS tracking of my watch, I can easily measure the length of the wave (noted $l$ below) and the amplitude (noted $\Delta$ below).

Based on these values, how much additional distance is reported by my watch? And consequently, how should I correct for reported distance and speed to find my actual performance?

The stupid way

Let’s approximate the pattern of oscillation by a sinusoidal function. We can note that in the case of a sinus with wave length $2l$, the same pattern of length $0.5 l$ is repeated 4 times:

And so we can zoom on that part and apply some basic math to see how much additional distance $dy$ is reported for a small increment $dx$:

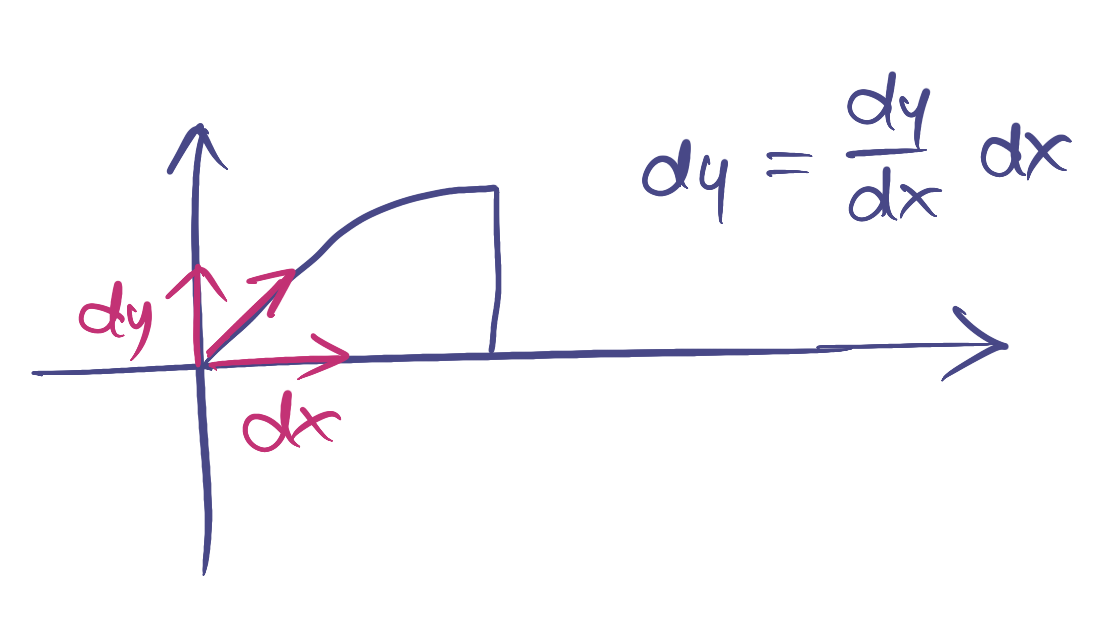
Since we assumed that the GPS tracking produce a sinus of amplitude $\Delta$ and wave length $2l$, we have:

$\displaystyle y(x) = \Delta sin \big(\frac{\pi}{l} x \big)$

And therefore the small increment is:

$\displaystyle \frac{dy}{dx} = \Delta \frac{\pi}{l} cos (\frac{\pi}{l} x \big)$

To find out how much additional distance is overestimated over the segment of length $0.5 l$, we integrate this small displacement:

$\displaystyle T = \int_0^{0.5 l} \Delta \frac{\pi}{l} cos (\frac{\pi}{l} x \big) dx = \Big[ \Delta sin \big(\frac{\pi}{l} x \big) \Big]_0^{0.5 l}$

$\displaystyle T = \Delta sin \big(\frac{\pi}{l} \frac{l}{2} \big) = \Delta sin \frac{\pi}{2} = \Delta$

And so for a real distance $l$, the smart watch will report me $l + 2 \Delta$ leads to an overestimation ratio equal to:

$\displaystyle r = \frac{l + 2 \Delta}{l} = 1 + 2 \frac{\Delta}{l}$

And I simply need to divide the reported distance (and speed!) by this ratio to get a corrected estimate of my real performance.

Oh wait… what did I just do?

Did you feel that we complicated our work for nothing above? Does the derivative followed by an integral sound just stupid? It’s because it is.

As it turns out, we can derive the same result in a much simpler way. Since we now that on this portion of the curve $y(x)$ is continuous and monotonous, we know that the additional distance is $\Delta$:

There is simply no other way: $y$ has to go through $\Delta$ distance. We therefore find that for every $0.5 l$ actual distance, the watch adds $\Delta$ to it, leading to the same result as before:

$\displaystyle r = \frac{0.5 l + \Delta}{0.5 l} = 1 + 2 \frac{\Delta}{l}$

The interesting thing to notice is that this does not depend on the actual shape of the curve: as long as the segment considered is such that $y(x)$ is monotonous and continuous, we get the same result.

Practical case

In my case, I noticed that the wave length was approximately 100 meters to 200 meters depending on the segments, with the amplitude being of the width of the road, so let’s say approximatively 5 meters.

And so we have $l = 50$ (or $l = 100$ for the 200 meters case) and $\Delta = 5$, leading to:

$\displaystyle r_{high} = 1 + 2 \frac{\Delta}{l} = 1 + 2 \frac{5}{50} = 1.2$

$\displaystyle r_{low} = 1 + 2 \frac{\Delta}{l} = 1 + 2 \frac{5}{100} = 1.1$

On those segments where my watch does this weird behavior, it report 10% to 20% more distance than what I really do!